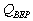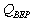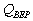Problems

1. The Crystal Sparkle Co. produces glass tumblers. The plant Is designed to produce 400 tumblers per hour, and there is one eight-hour shift per working day. However, the plant does not operate for the full eight hours: the employees take two 15-minute breaks in each shift, one in the first four hours and one in the second four hours, the first thirty minutes of the shift are spent raising the kilns to the required temperature for firing glass. The plant usually produces about 10,000 tumblers per five-day workweek. Answer the following questions by adjusting the data to one eight-hour shift.

1. What is the design capacity in tumblers?
2. What is the effective capacity in tumblers? As a percent?
3. What is the actual output in tumblers?
4. What is the efficiency?
5. What is the utilization?

2. The Goode and Cooke Company produces several models of frying pans. There is little difference in the production time required for the various models; the plant is designed to produce 160 frying pans per eight-hour shift, and there are two shifts per working day. However, the plant does not operate for the full eight hours: the employees take two 12-minute breaks in each shift, one in the first four hours and one in the second four hours; two hours per week are devoted to cleaning the factory and performing maintenance on the machines; one four-hour period every four weeks is devoted to the meeting of the quality circle. The plant usually produces about 3,500 frying pans per four-week period. You may ignore holidays in solving this problem. Answer the following questions by adjusting the data to a four-week time period.

1. What is the design capacity in frying pans?
2. What is the effective capacity in frying pans? As a percent?
3. What is the actual output?
4. What is the efficiency?
5. What is the utilization?
6. Re-work the problem using a time period of one eight-hour shift.

3. The selling price of the product is $199.95. The variable costs per unit are:

The fixed costs total $300,000 per year. Perform a breakeven analysis of this company.

1. What is the total revenue function?
2. What is the total cost function?
3. What is the profit function?
4. What is the breakeven point in units of the product?
5. What is the revenue at the breakeven point?
6. What is the income at the breakeven point?
7. Estimate the profit when 9,000 units of the product are sold in a year.
8. How many units must be sold for the company to make $900,000?

4. The Lade & Bach Company produces office chairs. The price of the chairs is $99.75 and the variable cost per chair is $49.75. The following fixed costs are incurred:

Perform a breakeven analysis of this company:

1. What is the total revenue function?
2. What is the total cost function?
3. What is the profit function?
4. What is the breakeven point in number of chairs?
5. What is the revenue at the breakeven point?
6. What is the income at the breakeven point?
7. Estimate the profit when 1,500 chairs are produced in a year.
8. How many chairs must be sold for the company to make $75,000 in a year?

5. (One step beyond) PC Fun & Games, Inc., produces a game for personal computers on a CD-ROM disk, which is entitled: Armageddon, the Final Battle. The company sells the disk to software retailers for $20.00, each, with a 5% discount for orders of 100 copies or more; virtually every retailer takes the discount. The variable costs of producing the disks are low, totaling only $7.00 each for the blank disk onto which the game is copied, the wages of the machine operator, and the packaging.

The game has become a best seller, and the production manager must plan to expand the capacity of the plant to turn out CD-ROM disks. CD-ROM disks are produced on a machine which makes copies of a master disk, one at a time. Each copy takes fifteen minutes, which includes inserting the blank disk, imprinting the game, and removing the finished disk.

At present, the Company has four machines; each machine cost $80,000 and has a service life of five years. The Company operates two eight-hour shifts per day, 50 weeks per year, and the machines require servicing and adjustments for one hour every day.

New machines can be purchased for $85,000. They also have a service life of five years and require one hour of servicing, but they can make copies in ten minutes. Because of the savings in copying time, the variable cost will drop to $6.00 per disk.

1. What is the annual effective capacity of one present machine?
2. What is the annual depreciation expense of one present machine? (Use straight line depreciation expense = cost/service life.)
3. What is the present breakeven point?
4. What is the annual effective capacity of one new machine?
5. What will be the annual effective capacity of the plant if one new machine is purchased?
6. What will be the new average variable cost per unit?
7. What will be the new breakeven point?
8. Suppose a second new machine is purchased. What will be the annual capacity of the plant?
9. What will be the new average variable cost per unit?
10. What will be the new breakeven point?

Solutions

1. a. Design capacity = 8 hrs. x 400 tumblers = 3,200 tumblers per 8-hour shift.
b. Effective capacity = Design capacity - Nonproductive activities.
Design capacity 8.0 hrs.
Less: Breaks .5 hrs.
Heat-up .5 hrs.
Net productive time 7.0 hrs.
Effective capacity = 7 hrs. x 400 tumblers = 2,800 tumblers.
Effective capacity percent = (100)(2800)/3200 = 87.5%.
c. Actual output = 10,000/5 = 2,000 tumblers per 8-hour shift. (This is a mean output. In reality there will be variation; some shifts will exceed 2,000 tumblers and some will fall short.)
d. Efficiency = Actual output/Effective capacity = (100)(2000)/2800 = 71.43%.
e. Utilization = Actual output/Design capacity = (100)(2000)/3200 = 62.50%.

2. a. Design capacity = 160 frying pans x 2 shifts x 20 working days = 6,400 frying pans per four weeks.
b. 160/8 = 20 frying pans per hour.
8 hrs. x 2 shifts x 20 working days = 320 hrs. available.
Less)
Breaks: (12 min. x 2 per shift x 2 shifts x 20 working days)/60 = 16 hrs.
Cleaning: 2 hrs. x 4 weeks 8 hrs.
Quality Circle 4 hrs.

Therefore, Net productive time is: 292 hrs.
Effective capacity = 292 hrs. x 20 frying pans = 5,840 frying pans per four weeks.
Effective capacity percent = (100)(5840)/6400 = 91.25%

c. Actual output = 3,500 frying pans.
d. Efficiency = Actual output/Effective Capacity = (100)(3500)/5840 = 59.93%.
e. Utilization = Actual output/Design capacity = (100)(3500)/6400 = 54.69%.
f. In terms of one 8-hour shift: Design capacity = 160 frying pans.
Effective capacity = 5840/40 = 146 frying pans.
The percentage answers will be the same as above.

3. a. Total Revenue = R x Q = 199.95Q.
b. Total cost = FC + VC x Q = 300000 + (60.25 + 25.70 + 21.50 + 17.50)Q = 300000 + 124.95Q.
c. Profit per year = R x Q - (VC x Q + FC) = 199.95Q - 124.95Q - 300000 = 75Q - 300000.
d. 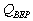<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Image175::/sites/dl/free/0072443901/24520/Image175.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Image175 (0.0K)</a>Image175 = FC/(R - VC) = 300000/75 = 4,000 units.
e. Revenue at the break-even point = 4000(199.95) = $799,800.
f. Income at the break-even point = $0.
g. Profit at 9,000 units = 75(9000) - 300000 = $375,000.
h. Number of units = (SP + FC)/(R - VC) = (900000 + 300000)/75 = 16,000 units.

4. a. Total revenue = R x Q = 99.75Q.
b. Total cost = FC + VC x Q = 94400 + 49.75Q.
c. Profit per year = R x Q - (VC x Q + FC) = 99.75Q - (49.75Q + 94400) = 50Q - 94400.
d. Q_BEP = FC/(R - VC) = 94400/50 = 1,888 chairs.
e. Revenue at the break-even point = 99.75(1888) = $188,328.
f. Income at the break-even point = $0.
g. Profit at 1,500 chairs = 50(1500) - 94400 = -$19,400, which is a net loss.
h. Number of chairs = (SP + FC)/(R - VC) = (94400 + 75000)/50 = 3,388 chairs.

5. a. Capacity = 4 disks/hr. x 15 hrs./day x 250 days/yr. = 15,000 disks/yr.
b. Depreciation = cost/service life = $80,000/5 yrs. = $16,000.
c. 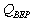<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Image176::/sites/dl/free/0072443901/24520/Image176.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Image176 (0.0K)</a>Image176 = FC/(R - VC) = 4($16,000)/($19 - $7) = 5,333disks.
d. Capacity = 6 disks/hr. x 15 hrs./day x 250 days/yr. = 22,500 disks/yr.
e. Capacity = 4(15,000) + 1(22,500) = 82,500 disks/yr.
f. VC = [$7(60,000) + $6(22,500)]/82,500 = $6.727.
g. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Image177::/sites/dl/free/0072443901/24520/Image177.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Image177 (0.0K)</a>Image177 = FC/(R - VC) = [4($16,000) + 1($17,000)]/($19 - $6.727) = 6,600 disks.
h. Capacity = 4(15,000) + 2(22,500) = 105,000 disks/yr.
i. VC = [$7(60,000) + $6(45,000)]/105,000 = $6.571.
j. 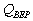<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Image178::/sites/dl/free/0072443901/24520/Image178.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Image178 (0.0K)</a>Image178 = FC/(R - VC) = [4($16,000) + 2($17,000)]/($19 - $6.571) = 7,885 disks.