Read Me - Difference of Squares Instructions (Word Format) (101.0K)

The Math Investigator is a data collection software program that may be used to collect data for the investigation. You may type answers onto the Word file or copy and paste in data from the Investigator.

Math Investigator 2.3

DIFFERENCE OF SQUARES on the Math Investigator determines the ways, if any, that a number can be written as the difference of two square numbers.

The number 65 is the difference of the two square numbers, 81 and 16:

81 - 16 = 65

Square numbers can be illustrated as square arrays of tiles. The difference between 81 and 16 is illustrated below by the shaded L-shaped region.

1. Investigate the whole numbers less that 50 to determine which numbers can and cannot be written as the difference of two square numbers. You may wish to print these numbers and their differences from the computer to find patterns. Form conjectures based on your observations. Test your conjectures on other numbers.
2. Select some odd numbers and for each one find pairs of squares whose difference equals the odd number. Find a pattern and form a conjecture. Test your conjecture on large odd numbers.
3. Summarize your observations and conjectures. Apply your conjectures to determine if numbers such as 1024, 2076, or 2077 are the difference of two squares. Use the Math Investigator to check your predictions.
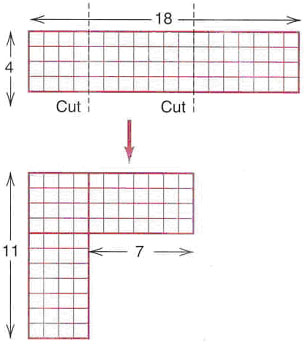
4. One way to see that 72 can be written as the difference of two squares is to represent 72 as a 4 by 18 array of tiles, make two cuts, and rearrange the pieces into an L-shape to show that 72 = 121 - 49, as shown below . Can such cuts in a rectangular array of tiles be made to form an outer and inner square if 72 is represented as a 3 by 24 array of tiles? Try this method on some numbers that can not be represented as the difference of two squares.