
In this chapter we considered how financing can be incorporated into the valuation of projects and ongoing businesses. There are two ways to take financing into account. The first is to calculate NPV by discounting at an adjusted discount rate, usually the after-tax weighted-average cost of capital (WACC). The second approach discounts at the opportunity cost of capital and then adds or subtracts the present values of financing side effects. The second approach is called adjusted present value, or APV.
The formula for the after-tax WACC is:
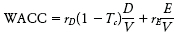
where rD and rE are the expected rates of return demanded by investors in the firm's debt and equity securities, D and E are the current market values of debt and equity, and V is the total market value of the firm (V = D + E). Of course, the WACC formula expands if there are other sources of financing, for example, preferred stock.
Strictly speaking, discounting at WACC works only for projects that are carbon copies of the existing firm—projects with the same business risk that will be financed to maintain the firm's current, market debt ratio. But firms can use WACC as a benchmark rate to be adjusted for differences in business risk or financing. We gave a three-step procedure for adjusting WACC for different debt ratios.
Discounting cash flows at the WACC assumes that debt is rebalanced to keep a constant ratio of debt to market value. The amount of debt supported by a project is assumed to rise or fall with the project's after-the-fact success or failure. The WACC formula also assumes that financing matters only because of interest tax shields. When this or other assumptions are violated, only APV will give an absolutely correct answer.
APV is, in concept at least, simple. First calculate the base-case NPV of the project or business on the assumption that financing doesn't matter. (The discount rate is not WACC, but the opportunity cost of capital.) Then calculate the present values of any relevant financing side effects and add or subtract from base-case value. A capital investment project is worthwhile if
APV = base-case NPV + PV(financing side effects)
is positive. Common financing side effects include interest tax shields, issue costs, and special financing packages offered by suppliers or governments.
For firms or going-concern businesses, value depends on free cash flow. Free cash flow is the amount of cash that can be paid out to all investors, debt as well as equity, after deducting cash needed for new investment or increases in working capital. Free cash flow does not include the value of interest tax shields, however. The WACC formula accounts for interest tax shields by using the after-tax cost of debt. APV adds PV(interest tax shields) to base-case value.
Businesses are usually valued in two steps. First free cash flow is forecasted out to a valuation horizon and discounted back to present value. Then a horizon value is calculated and also discounted back. The horizon value is usually estimated by using the perpetual-growth DCF formula or by multiplying forecasted EBIT or EBITDA 26 by multiples observed for similar firms. Be particularly careful to avoid unrealistically high horizon values. By the time the horizon arrives, competitors will have had several years to catch up. Also, when you are done valuing the business, don't forget to subtract its debt to get the value of the firm's equity.
All of this chapter's examples reflect assumptions about the amount of debt supported by a project or business. Remember not to confuse "supported by" with the immediate source of funds for investment. For example, a firm might, as a matter of convenience, borrow $1 million for a $1 million research program. But the research is unlikely to contribute $1 million in debt capacity; a large part of the $1 million new debt would be supported by the firm's other assets.
Also remember that debt capacity is not meant to imply an absolute limit on how much the firm can borrow. The phrase refers to how much it chooses to borrow against a project or ongoing business.