
In this chapter we have used our newfound knowledge of present values to examine the market price of common stocks. The value of a stock is equal to the stream of cash payments discounted at the rate of return that investors expect to receive on other securities with equivalent risks.
Common stocks do not have a fixed maturity; their cash payments consist of an indefinite stream of dividends. Therefore, the present value of a common stock is
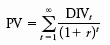
However, we did not just assume that investors purchase common stocks solely for dividends. In fact, we began with the assumption that investors have relatively short horizons and invest for both dividends and capital gains. Our fundamental valuation formula is, therefore,
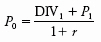
This is a condition of market equilibrium. If it did not hold, the share would be overpriced or underpriced, and investors would rush to sell or buy it. The flood of sellers or buyers would force the price to adjust so that the fundamental valuation formula holds. We also made use of the formula for a growing perpetuity presented in Chapter 2. If dividends are expected to grow forever at a constant rate of g, then

It is often helpful to twist this formula around and use it to estimate the market capitalization rate r, given P0 and estimates of DIV1 and g:
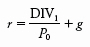
Remember, however, that this formula rests on a very strict assumption: constant dividend growth in perpetuity. This may be an acceptable assumption for mature, low-risk firms, but for many firms, near-term growth is unsustainably high. In that case, you may wish to use a two-stage DCF formula, where near-term dividends are forecasted and valued, and the constant-growth DCF formula is used to forecast the value of the shares at the start of the long run. The near-term dividends and the future share value are then discounted to present value.
The general DCF formula can be transformed into a statement about earnings and growth opportunities:
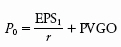
The ratio EPS 1 / r is the capitalized value of the earnings per share that the firm would generate under a no-growth policy. PVGO is the net present value of the investments that the firm will make in order to grow. A growth stock is one for which PVGO is large relative to the capitalized value of EPS. Most growth stocks are stocks of rapidly expanding firms, but expansion alone does not create a high PVGO. What matters is the profitability of the new investments.
The same formulas that we used to value common shares can also be used to value entire businesses. In that case, we discount not dividends per share but the entire free cash flow generated by the business. Usually a two-stage DCF model is deployed. Free cash flows are forecasted out to a horizon and discounted to present value. Then a horizon value is forecasted, discounted, and added to the value of the free cash flows. The sum is the value of the business.
Valuing a business is simple in principle but not so easy in practice. Forecasting reasonable horizon values is particularly difficult. The usual assumption is moderate long-run growth after the horizon, which allows use of the growing-perpetuity DCF formula at the horizon. Horizon values can also be calculated by assuming “normal” price–earnings or market-to-book ratios at the horizon date.
In earlier chapters you should have acquired—we hope painlessly—a knowledge of the basic principles of valuing assets and a facility with the mechanics of discounting. Now you know something of how common stocks are valued and market capitalization rates estimated. In Chapter 5 we can begin to apply all this knowledge in a more specific analysis of capital budgeting decisions.