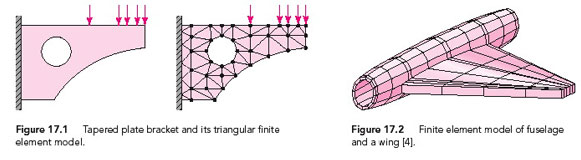
In real design problems, generally structures are composed of a large assemblage of various members. In addition, the built-up structures or machines and their components involve complicated geometries, loadings, and material properties. Given these factors, it becomes apparent that the classical methods can no longer be used. For complex structures, the designer has to resort to more general approaches of analysis. The most widely used of these techniques is the finite element stiffness or displacement method. Unless otherwise specified, we refer to it as the finite element method (FEM).

Finite element analysis (FEA) is a numerical approach and well suited to digital computers. The method is based on the formulations of a simultaneous set of algebraic equations relating forces to corresponding displacements at discrete preselected points (called nodes) on the structure. These governing algebraic equations, also referred to as forcedisplacement relations, are expressed in matrix notation [1]. With the advent of high-speed, large-storage capacity digital computers, the finite element method gained great prominence throughout the industries in the solution of practical analysis and design problems of high complexity. The literature related to the FEA is extensive (for example, [2-20]). Numerous commercial FEA software programs are available, including some directed at the learning process. Most of the developments have now been coded into commercial programs.

The basic concept of the finite element approach is that the real structure can be discretized by a finite number of elements, connected not only at their nodes but along the interelement boundaries as well. Usually, triangular or rectangular shapes of elements are used in the finite element method. Figure 17.1 depicts how a real structure is modeled using triangular element shapes. The types of elements commonly employed in structural idealization are the truss, beam, two-dimensional elements, shell and plate bending, and threedimensional elements. Asolid model of an aircraft structure created using beam, plate, and shell elements is shown in Figure 17.2. Note that, in the analysis of large structural systems, such as ships, multistory buildings, or aircraft, the storage capacity of even generalpurpose programs can sometimes be overrun. It may be necessary to use the method of substructures that divides the original system into smaller units. Once the stiffness of each substructure has been determined, the analysis of the system follows the familiar procedure of matrix methods used in structural mechanics.

<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg:: ::/sites/dl/free/007242155x/69912/chap17out_figure1.jpg','popWin', 'width=631,height=230,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (22.0K)</a>

To adequately treat the subject of the FEA would require a far more lengthy presentation than could be justified here. Nevertheless, the subject is so important that any engineer concerned with the analysis and design of members should have at least an understanding of FEA. The fundamentals presented can clearly indicate the potential of the FEA as well as its complexities. It can be covered as an option, used as a "teaser" for a student’s advance study of the topic, or as a professional reference. For simplicity, only four basic structural elements are discussed here: the one-dimensional axial element or truss element, the beam element or plane frame element, two-dimensional element, and the axisymmetric element. Sections 17.3, 17.5, and 17.8 present the formulation and general procedure for treating typical problems by the finite element method. Solutions of axial stress, plane stress, and axisymmetrical problems are demonstrated in various examples and case studies.