Problems

1. Here is a payoff matrix; parentheses designate a loss. The probabilities of the states of nature, p(1) and p(2), are unknown.

1. Which alternative should be selected under the maximax criterion?
2. Which alternative should be selected under the maximin criterion?
3. Which alternative should be selected under the Laplace criterion?
4. What is the opportunity loss table?
5. Which alternative should be selected under the minimax regret criterion?

2. Refer to Problem 1. Construct the sensitivity graph, as shown on p. 207 of your textbook.

1. For what range of values of p(2) is alternative A preferred?
2. For what range of values of p(2) is alternative B preferred?
3. For what range of values of p(2) is alternative C preferred?

3. Fall has come, and the department manager of the Purple Pentagon Discount Store must decide how many snow blowers to order for the winter season. He believes there is an association between the weather and the demand for snow blowers: a winter with heavy snow should produce a high demand, and a winter with light snow should produce a low demand. However, if he guesses wrong and orders a large number of snow blowers when the weather turns out to have light snow, he will suffer a loss. Here is his payoff matrix.

1. Which alternative should be selected under the maximax criterion?
2. Which alternative should be selected under the maximin criterion?
3. Which alternative should be selected under the Laplace criterion?
4. What is the opportunity loss table?
5. Which alternative should be selected under the minimax regret criterion?

4. Refer to Problem 3. Suppose that the following probabilities are available regarding the snowfall next winter:
p(heavy snow) = .10
p(medium snow) = .50
p(light snow) = .40

1. Which alternative should be selected under the expected value criterion?
2. Which alternative should be selected under the lowest expected loss criterion?
3. What is the value of the EVPI?
4. What is the interpretation of the EVPI?

5. Solve problem #4 by using an EXCEL spreadsheet.

1. Find the expected monetary values.
2. Find the largest expected monetary value.
3. Find the expected value of perfect information.
4. Compare the answers on your spreadsheet to the answers to problem #4.

6. (One step beyond) The telephone company has three billing plans.

1. An unlimited number of local telephone calls per month for $20.00
2. Fifty (or fewer) local telephone calls per month for $16.00 plus $0.08 per call above 50 calls.
3. Twenty (or fewer) local telephone calls per month for $12.00 plus $0.10 per call above 20 calls.

1. What is the payoff table?
2. Which plan should be selected under the minimax regret criterion?
3. Why is it improper to use the maximax criteria here?
4. Suppose that the subscriber assesses probabilities as follows:
   p(60 calls) = .40 p(120 calls) = .20
   p(90 calls) = .30 p(160 calls) = .10
   Which plan should be selected under the best expected value criterion?
5. Which plan should be selected under the least expected regret criterion?

Solutions

1. a. The maximax criterion involves selecting the best payoff for each alternative and then selecting the best payoff in that set.

Implement Alternative B.

b. The maximin criterion involves selecting the worst payoff for each alternative and then selecting the best payoff in that set.

Implement Alternative A.

c. The LaPlace criterion involves selecting the best mean payoff.

Implement Alternative A or Alternative B.

*Note: (500 + 300)/2 = 400.

d. Find the regret for each cell by subtracting each entry in the state of nature column from the maximum entry in the column.

e. The minimax regret criterion involves selecting the worst regret for each alternative, and then selecting the best of that set.

Implement Alternative A.

At the points where the lines in the diagram intersect the y coordinates are equal; y = a + bx, where a is the intercept on the (1) column and b = payoff #2 - payoff #1.

A line: y = 500 + (300 - 500)x = 500 - 200x.
B line: y = 700 + (100 - 700)x = 700 - 600x.
C line: y = -300 + (600 - (-300))x = -300 + 900x.

The A line and the B line intersect.

500 - 200p(2) = 700 - 600p(2)
-200 = -400p(2)
p(2) = 0.5
p(1) = 1 - p(2) = 1 - 0.5 = 0.5.

The A line and the C line intersect.

500 - 200p(2) = -300 + 900p(2)
800 = 1100p(2)
p(2) = 0.727
p(1) = 1 - p(2) = 1 - 0.727 = .273.

a. Choose A for 0.5 < p(2) < 0.727.
b. Choose B for 0 < p(2) < 0.5.
c. Choose C for 0.727 < p(2) < 1.0.

3. a.

Place a large order.

b.

Place a small order.

c.

Place a medium order.

*Note: (5000 + 1000 - 4000)/3 = 667.

d. Find the regret for each cell in the payoff matrix by subtracting each entry in the state of nature column from the maximum payoff in the column. For the Heavy Snow column, the best payoff is $5,000, and the regrets are 0, $3,000, and $4,500.

e.

Place a medium order.

*Note: (5000 + 1000 - 4000)/3 = 667.

d. Find the regret for each cell in the payoff matrix by subtracting each entry in the state of nature column from the maximum payoff in the column. For the Heavy Snow column, the best payoff is $5,000, and the regrets are 0, $3,000, and $4,500.

e.

Place a medium order.

*Note: 5000(.10) + 1000(.50) - 4000(.40) = -600.

b.

*Note: 0(.10) + 2000(.50) + 5000(.40) = 3000.
Place a medium order. The strategy which is selected by the least expected loss criterion
will always be the same as the one selected by the best expected value criterion.

c. EVPI = least expected loss = $1,500.
d. $1,500 is the absolute maximum which might be spent to obtain information about the states
of nature. The manager might, for example, hire a weather forecaster to forecast next
winter's snowfall.

5.

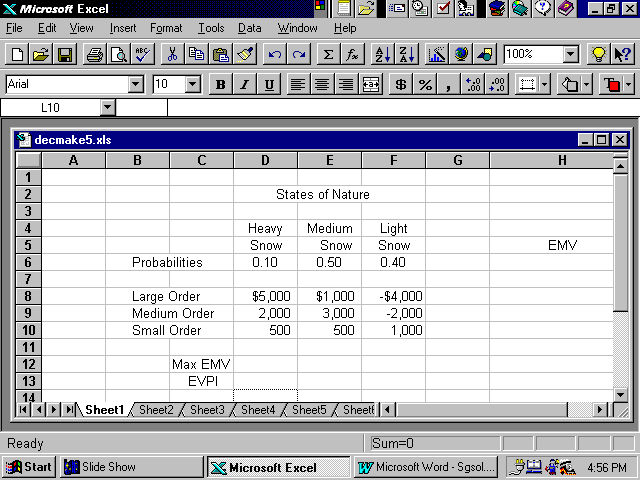<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Image179::/sites/dl/free/0072443901/24520/Image179.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Image179 (21.0K)</a>Image179

1. In Cell H-8: =D6*D8+E6*E8+F6*F8
In Cell H-9: =D6*D9+E6*E9+F6*F9
In Cell H-10: =D6*D10+E6*E10+F6*F10
2. In Cell D-12: =MAX(H8:H10)
3. In Cell D-13: =MAX(D8:D10)*D6+MAX(E8:E10)*E6+MAX(F8:F10)*F6-D12
4. Did you get the same answers as in #4-a and #4-c?

6. a. It is necessary to estimate the total cost of each possible number of calls under each billing plan.

Plan a) The cost will be $20, regardless of the number of calls.

Plan b) The cost will be $16 + (number of calls - 50) x $0.08, when there are more than 50 calls.
Plan c) The cost will be $12 + (number of calls - 20) x $0.10, when there are more than 20 calls.

The payoff table will be:

b. Select the best payoff for each state of nature; they are 16.00, 19.00,20.00, and 20.00.

Subtract every entry in the column from the best entry. The differences are the regrets.

Pick the worst regret for each alternative:

Alternative Worst Regret
Plan a 4.00 (best)
Plan b 4.80
Plan c 6.00
The subscriber should select Plan a.

c. It is improper to use the maximax criterion here because the payoffs are expenses rather than incomes.
d. Incorporate the probabilities into the payoff table and calculate the expected value of each plan.

The subscriber should select Plan c.
*Note: (16.80)(.40) + (19.20)(.30) + (21.60)(.20) + (24.80)(.10) = 19.28.

e. The subscriber should select Plan c.