
(See related pages)
| The Investigation poses questions to generate interest in various mathematical topics from the text and encourages students to formulate and investigate their own conjectures. One use of the investigations is for term papers in which students report on their conjectures and the patterns they find.
Click on the Read Me file below to open the investigation in a Word file: Computer Investigation 10.1Measuring Angles and Areas*Starting Points for Investigations 1. An inner triangle has been formed in the following figure whose vertices are the midpoints of the sides of the larger triangle. 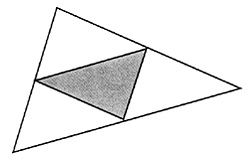 a. What relationships are there between the inner triangle and the larger triangle? b. If the midpoints of the sides of an arbitrary quadrilateral are the vertices of an inner quadrilateral, what relationships are there between the smaller and larger quadrilateral? c. Continue this investigation by forming inner polygons whose vertices are the midpoints of the sides of pentagons, hexagons, and in general, polygons with increasing numbers of sides. Describe any relationships you find. 2. The square below is subdivided into three regions by segments BX and BY. 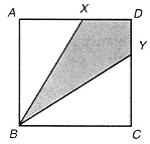 a. If points X and Y are located so that Δ ABX, quadrilateral BYXD, and Δ ABX have the same area, what is the measure of ∠XBY? b. Investigate the question in part a for regular polygons with a greater number of sides. Form a conjecture about the measures of ∠XBY for these polygons. c. Investigate the question in part a for a circle. That is, what is the measure of ∠XBY if the areas of the three regions formed by segments BX and BY are equal? How does the measure of this angle compare to the measures of the angles in part b? 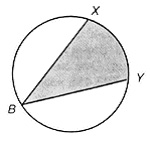 *This investigation may be carried out with software such as Cabri Geometry II, Geometer's Sketch Pad, or The Geometric Super Supposer. |