Read Me - Integer Differences Instructions (Word Format) (61.0K)

The Math Investigator is a data collection software program that may be used to collect data for the investigation. You may type answers onto the Word file or copy and paste in data from the Investigator.

Math Investigator 5.1

INTEGER DIFFERENCES on the Math Investigator computes the differences of consecutive pairs of integers at adjacent vertices (corners) of a k-sided polygon, and repeats the process as many times as desired.

Select any four integers and place then at the vertices (corners) of a square. Then between each pair of integers write the difference of the larger minus the smaller and form an inner square whose vertices have these differences. Continue this process of taking differences and forming inner squares. Will this process result in an inner square of all zeros? (Observations in the 1930's concerning this investigation are attributed to the Italian mathematician E. Ducci.)

1. If you begin with the larger square shown below, how many inner squares must be formed before obtaining a square with all zeros? Try other integers at the four vertices to see if an inner square with all zeros can always be obtained. Form a conjecture and test it on some other numbers.
<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072533072/78572/5_1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (24.0K)</a> 
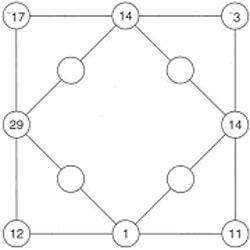2. Try this investigation by beginning with 3 numbers at the vertices of a triangle. Will an inner triangle of all zeros always be obtained? What patterns can you find? Form conjectures involving the process of computing differences by using numbers at the vertices of a triangle.
3. Any integer k for k > 3 may be selected and placed at the vertices of a k-sided polygon. Investigate the problem of obtaining inner polygons of all zeros for polygons with 5 sides (pentagons), 6 sides (hexagons), 7 sides (heptagons), and 8 sides (octagons). Use your observations to form conjectures.