|
| 1 | The rules for computing equivalent resistance are the same as those for
computing equivalent capacitance. |
 | A) | True |
 | B) | False |
|
| 2 | The current is the same in all parts of a parallel circuit. |
 | A) | True |
 | B) | False |
|
| 3 | The equivalent resistance of two resistors in parallel is equal to their product divided by their sum. |
 | A) | True |
 | B) | False |
|
| 4 | The emf is essentially equal to the open-circuit potential difference. |
 | A) | True |
 | B) | False |
|
| 5 | The current supplied to an electric circuit is equal to the net emf divided by the total resistance of the circuit if we neglect internal resistance. |
 | A) | True |
 | B) | False |
|
| 6 | Kirchhoff’s second law applies for each current loop in a complex circuit and not just for the total circuit. |
 | A) | True |
 | B) | False |
|
| 7 | In applying Kirchhoff’s laws, the tracing direction must be the same as the current direction. |
 | A) | True |
 | B) | False |
|
| 8 | When the Wheatstone bridge is balanced, the voltage between the galvanometer and either terminal of the source of emf will be the same. |
 | A) | True |
 | B) | False |
|
| 9 | Kirchhoff’s laws apply only for current loops that contain at least one source of emf. |
 | A) | True |
 | B) | False |
|
| 10 | When two identical resistors are connected in parallel, the voltage drop across each is one-half of the terminal potential difference at the source of emf. |
 | A) | True |
 | B) | False |
|
| 11 | The variance of terminal potential difference, as compared with emf, is due to |
 | A) | the circuit load |
 | B) | the internal resistance |
 | C) | Kirchhoff’s law |
 | D) | current delivered |
|
| 12 | For a parallel circuit, which of the following is not true? |
 | A) | The current through each resistance is the same. |
 | B) | The voltage across each resistance is the same. |
 | C) | The total current is equal to the sum of the currents through each resistance. |
 | D) | The reciprocal of the equivalent resistance is equal to the sum of the reciprocals of the individual resistances. |
|
| 13 | Which of the following is not affected by internal resistance? |
 | A) | Terminal potential difference |
 | B) | Source emf |
 | C) | Current delivered to external circuit |
 | D) | Power output |
|
| 14 | If a circuit contains three loops, how many independent equations can be obtained with Kirchhoff’s two laws? |
 | A) | Three |
 | B) | Four |
 | C) | Five |
 | D) | Six |
|
| 15 | When using the Wheatstone bridge, the quantity that is balanced is |
 | A) | voltage |
 | B) | resistance |
 | C) | current |
 | D) | emf |
|
| 16 | For the circuit in Fig. 28-4, the equivalent external resistance is approximately
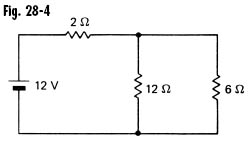 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig284.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig284.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> |
 | A) | 1.8 Ω |
 | B) | 4 Ω |
 | C) | 6 Ω |
 | D) | 20 Ω |
|
| 17 | In Fig. 28-4, if we neglect internal resistance, the current through the 6-Ω resistance is
 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig284.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig284.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> |
 | A) | 1.0 A |
 | B) | 1.33 A |
 | C) | 1.67 A |
 | D) | 2 A |
|
| 18 | The terminal voltage for the source of emf in Fig. 28-5 is
 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig285.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (17.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig285.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (17.0K)</a> |
 | A) | 24 V |
 | B) | 22 V |
 | C) | 21.8 V |
 | D) | 20 V |
|
| 19 | The current through the 4-Ω resistance in Fig. 28-6, as found from Kirchhoff’s laws is
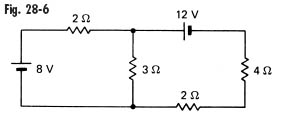 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig286.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077158733/294254/fig286.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> |
 | A) | 1 A |
 | B) | 1.5 A |
 | C) | 2 A |
 | D) | 2.5 A |
|
| 20 | A Wheatstone bridge is used to measure the unknown resistance Rx of a coil of wire. The resistance box is adjusted for 8 Ω, and the galvanometer indicates zero current when the contact key is positioned at the 40-cm mark. The unknown resistance is |
 | A) | 5.33 Ω |
 | B) | 12 Ω |
 | C) | neither (a) nor (b) |
 | D) | either (a) or (b) depending on hookup |

