| The Investigation poses questions to generate interest in various mathematical topics from the text and encourages students to formulate and investigate their own conjectures. One use of the investigations is for term papers in which students report on their conjectures and the patterns they find.
Click on the Read Me file below to open the investigation in a Word file:
 Read Me - Probability Machines Instructions (Word Format)
(49.0K) Read Me - Probability Machines Instructions (Word Format)
(49.0K)
Laboratory Investigation 8.2Probability Machines
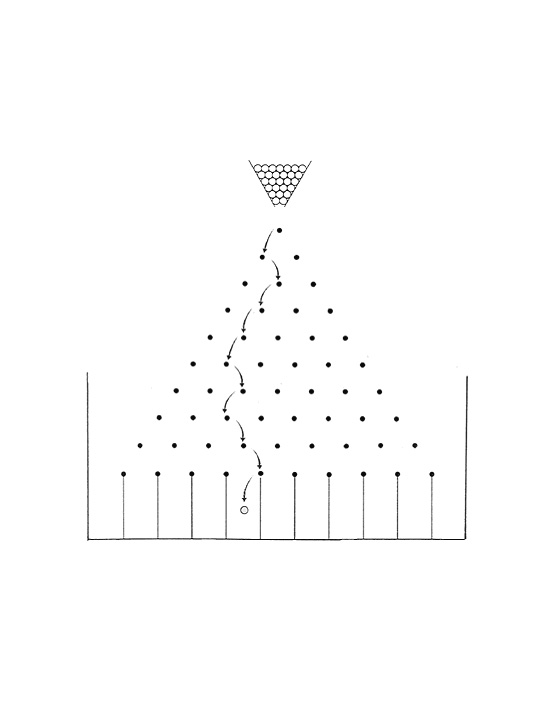
The device shown in the figure below is called a probability machine and was described by Sir Francis Galton in 1889. There are 10 horizontal rows of pegs in the top part of this device. As a ball falls through the opening at the top center, it strikes the center peg in the top row and has an equal chance of going right or left. At each lower row of pegs, the ball hits a peg and in each case it has a 50:50 chance of falling right or left. The balls collect in 11 compartments in the lower half of this device. When many balls are dropped, the distribution of the balls will be approximately normal, with the greatest number in the center compartment and the numbers of balls decreasing as the compartments become farther from the center.
 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_8_2a.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (32.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_8_2a.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (32.0K)</a>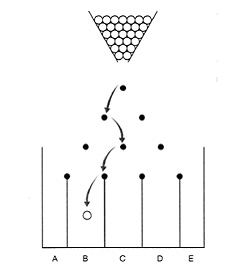 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_8_2b.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (23.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_8_2b.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (23.0K)</a> |


