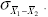|  Statistics for the Behavioral Sciences, 4/e Michael Thorne,
Mississippi State University -- Mississippi State
Martin Giesen,
Mississippi State University -- Mississippi State
Significance of the Difference Between Two Sample Means
Chapter OverviewThe chapter begins with the derivation of the sampling distribution of the differences for independent
samples. First, pairs of random samples are taken from a population, and means for some characteristic are
computed. Next, the difference between the pairs of means is determined. A frequency distribution of the
differences is constructed, and the distribution is used to plot a frequency polygon. The distribution is
called the sampling distribution of the mean differences.
The properties of the sampling distribution of the mean differences are (1) its mean is equal to 0;
(2) the larger the size of the samples drawn from the population, the more closely the sampling distribution
approximates the normal curve; (3) the larger the size of the samples, the smaller the standard deviation of
the sampling distribution. The standard deviation is called the standard error of the difference between
means and is symbolized by 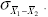 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/chap10.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a> Both raw-score and defining formulas for estimating the standard
error of the differences are given. The estimated standard error is symbolized by <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/chap10.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a> Both raw-score and defining formulas for estimating the standard
error of the differences are given. The estimated standard error is symbolized by  <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/10b.GIF','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a>
As in Chapter 9, hypothesis testing involves computing how far from the mean of the sampling
distribution our observed difference in sample means lies in estimated standard error units. We first
compute a t score and then compare the computed t score with values known to cut off the deviant 5% (or
1%) of the distribution of t for samples of a given size converted to degrees of freedom. The t score or t
ratio is the ratio of the difference between a pair of sample means to the estimated standard error of the
differences. The degrees of freedom for the t test for independent samples is N1 + N2 – 2, and the critical
values again are found in Table B.
A two-tailed test looks at both ends of the distribution of the test statistic, t in this chapter. Only one
end of the distribution is considered in the one-tailed test. The end considered in the one-tailed test is the
one predicted by the experimenter before conducting the experiment. The one-tailed test is a more powerful
test if the outcome of the experiment is in the predicted direction. If you can reasonably predict the
outcome’s direction before data collection, use of the one-tailed test is warranted because it is more
powerful. To determine the one-tailed probabilities, halve the probability values in Table B.
Assumptions required by the two-sample t test for independent samples are that the populations from
which the samples are drawn are normal, that the population variances are homogeneous (equal), and that
the samples are independent. The first two assumptions apparently can be violated with little effect upon
the conclusions made with the test. This property of a statistical test to give valid conclusions even when its
assumptions are violated is called robustness. If you fear violation of the assumptions, it is recommended
that you use fairly large samples of equal size.
The power of the test can be increased by using dependent samples. Dependent samples can be formed
by using matched pairs of unrelated individuals in which subject pairs, matched as closely as possible on
relevant characteristics, are selected. Then, one member of each pair is assigned to one treatment group,
and the other member is assigned to the other group. Another procedure for obtaining dependent samples is
to use each subject as his or her own control; that is, the same individuals are given each experimental
treatment. This type of experiment is called a repeated measures design or within-subjects comparison.
The power of the test using dependent samples is increased through a decrease in the standard
deviation of the sampling distribution of mean differences. The standard deviation is called the standard
error of the mean differences and is symbolized by <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/10b.GIF','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a>
As in Chapter 9, hypothesis testing involves computing how far from the mean of the sampling
distribution our observed difference in sample means lies in estimated standard error units. We first
compute a t score and then compare the computed t score with values known to cut off the deviant 5% (or
1%) of the distribution of t for samples of a given size converted to degrees of freedom. The t score or t
ratio is the ratio of the difference between a pair of sample means to the estimated standard error of the
differences. The degrees of freedom for the t test for independent samples is N1 + N2 – 2, and the critical
values again are found in Table B.
A two-tailed test looks at both ends of the distribution of the test statistic, t in this chapter. Only one
end of the distribution is considered in the one-tailed test. The end considered in the one-tailed test is the
one predicted by the experimenter before conducting the experiment. The one-tailed test is a more powerful
test if the outcome of the experiment is in the predicted direction. If you can reasonably predict the
outcome’s direction before data collection, use of the one-tailed test is warranted because it is more
powerful. To determine the one-tailed probabilities, halve the probability values in Table B.
Assumptions required by the two-sample t test for independent samples are that the populations from
which the samples are drawn are normal, that the population variances are homogeneous (equal), and that
the samples are independent. The first two assumptions apparently can be violated with little effect upon
the conclusions made with the test. This property of a statistical test to give valid conclusions even when its
assumptions are violated is called robustness. If you fear violation of the assumptions, it is recommended
that you use fairly large samples of equal size.
The power of the test can be increased by using dependent samples. Dependent samples can be formed
by using matched pairs of unrelated individuals in which subject pairs, matched as closely as possible on
relevant characteristics, are selected. Then, one member of each pair is assigned to one treatment group,
and the other member is assigned to the other group. Another procedure for obtaining dependent samples is
to use each subject as his or her own control; that is, the same individuals are given each experimental
treatment. This type of experiment is called a repeated measures design or within-subjects comparison.
The power of the test using dependent samples is increased through a decrease in the standard
deviation of the sampling distribution of mean differences. The standard deviation is called the standard
error of the mean differences and is symbolized by 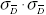 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/10c.GIF','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a> is estimated by <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/10c.GIF','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a> is estimated by  <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/10d.GIF','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (0.0K)</a> , which is called the
estimated standard error of the mean differences.
The direct difference method is used to compute a t ratio for dependent or related samples. In the final
equation discussed, t is computed by dividing the mean of the differences by the standard error of the mean
differences. The computed value of t is then compared with the critical values of t from Table B with df =
N – 1, where N is the number of pairs of scores. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55319/10d.GIF','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (0.0K)</a> , which is called the
estimated standard error of the mean differences.
The direct difference method is used to compute a t ratio for dependent or related samples. In the final
equation discussed, t is computed by dividing the mean of the differences by the standard error of the mean
differences. The computed value of t is then compared with the critical values of t from Table B with df =
N – 1, where N is the number of pairs of scores. |
|



 2003 McGraw-Hill Higher Education
2003 McGraw-Hill Higher Education