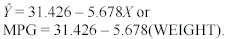|  Statistics for the Behavioral Sciences, 4/e Michael Thorne,
Mississippi State University -- Mississippi State
Martin Giesen,
Mississippi State University -- Mississippi State
Correlation and Regression
SPSS ExercisesUSING SPSS - EXAMPLES AND EXERCISES
SPSS provides procedures for both the Pearson and the Spearman correlation coefficients, as well as
procedures for simple and multiple regression. We will also show you how to obtain a scatterplot with
regression line to assist in visualizing the relationship between two measures and to check the assumption
of a linear correlation/regression relationship.Example-Pearson and Spearman Correlation Coefficients: We will use SPSS to work Problem 5.
First, let's assume that the dominance ratings are interval level measurement and compute the Pearson
correlation. After we complete that process, we will assume that the ratings are pure ranks (ordinal level
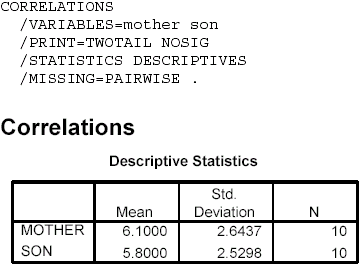
measurement) and calculate the Spearman correlation. Finally, we will obtain a scatterplot of the data. The steps are as follows:- Start SPSS and enter the data into variable columns named mother and son.
- Select Analyze > Correlate > Bivariate.
- Highlight and move both variables into the Variables box and select both the Pearson and Spearman boxes under Correlation Coefficients.
- Click Options > Means and Standard deviations > Continue > OK, and the results should appear in the output Viewer window.
- To obtain a scatterplot, select Graph>Scatter > Simple > Define.
- Highlight and move mother to the X-axis box and son to the Y-axis box; click OK, and the plot should appear in the output Viewer window.
Notes on Reading the Output- The Correlations box gives the results for the Pearson correlation as a matrix. The first number in the box is the correlation coefficient, r = .971; the next value is the significance of the correlation, p = .000 (p < .001); and the last value is the sample size, N = 10. Thus, the correlation is statistically significant. The Correlations box under the section labeled Nonparametric Correlations gives the Spearman correlation (rS = .925) using the same arrangement.
- In examining the scatterplot, remember that we never connect the points but look at the plot to confirm the sign and strength of the correlation and to check for a nonlinear pattern, which would be a possible violation of our assumption of a linear relationship. You might want to put an oval around the points to assist you in visualizing the relationship.
 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss1.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (9.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss1.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (9.0K)</a>  <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss2.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (21.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss2.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (21.0K)</a>  <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss3.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (5.0K)</a> Example - Regression:
Let's use SPSS to find the regression equation for Problem 7. Also, we will produce a scatterplot with a regression line. The procedure is as follows: <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss3.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (5.0K)</a> Example - Regression:
Let's use SPSS to find the regression equation for Problem 7. Also, we will produce a scatterplot with a regression line. The procedure is as follows:- Start SPSS and enter the data under the variable names weight and mpg.
- Select Analyze > Regression > Linear.
- Move mpg into the Dependent box and weight into the Independent(s) box; click Statistics > Descriptives (Estimates and Model fit should already be checked by default) > Continue > OK. The results should appear in the output Viewer window.
- To get the scatterplot, switch to the Data Editor window and follow the instructions in the previous example on producing it. Note that in a regression problem, we want the dependent variable-the measure we want to predict-to be plotted on the vertical (Y) axis, so mpg should appear on the Y axis.
- Once the scatterplot has appeared in the output Viewer window, double-click on the chart and maximize the chart window. In the Menu Bar, click Chart > Options. In the Scatterplot Options box, select Total > OK, and the regression line should appear on the graph. Because we are finished editing the chart, select File > Close to close the chart window. If necessary, switch to the output Viewer window, in which you should find the scatterplot with regression line.
Notes on Reading the Output- As with the previous examples, you should find the results relatively easy to identify and interpret in this output. The Coefficients box gives the intercept and slope terms in the column labeled B under the section labeled Unstandardized Coefficients. The term in the row labeled (Constant) is the intercept term, a = 31.426, and the term in the row labeled WEIGHT is the slope, b= -5.678. Thus, the regression equation could be written as follows:
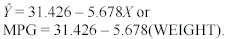 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss4.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (2.0K)</a> The scatterplot with regression line shows a close fit with no indication of nonlinearity. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss4.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (2.0K)</a> The scatterplot with regression line shows a close fit with no indication of nonlinearity. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss5.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (17.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss5.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (17.0K)</a>  <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss6.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (13.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss6.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (13.0K)</a> 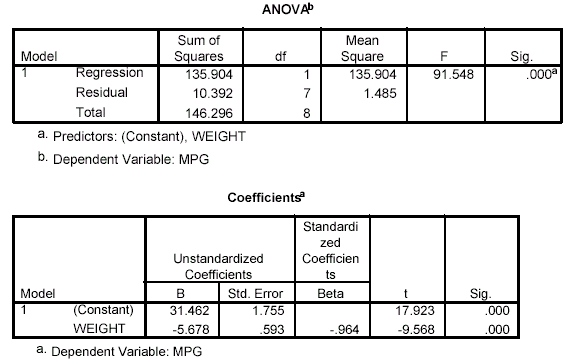 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss7.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (16.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss7.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (16.0K)</a> 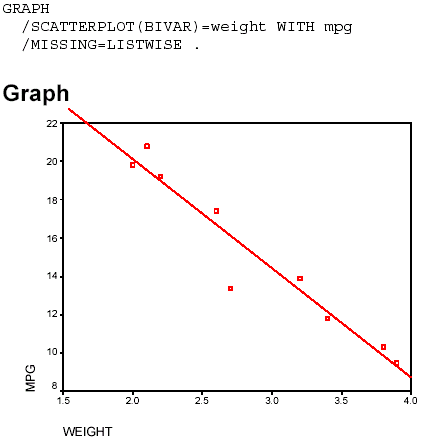 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss8.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (6.0K)</a> Exercises Using SPSS <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55322/c13_spss8.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (6.0K)</a> Exercises Using SPSS- Use SPSS to work Problem 6.
- Use SPSS and the data from Problem 6 to compute a regression equation predicting the current events score from time spent reading the newspaper. Give the regression equation and obtain a scatterplot with regression line.
- Use SPSS to work Problem 9, assuming the data are pure ranks. Obtain a scatterplot.
 Click here to view the answers. (107.0K) Click here to view the answers. (107.0K)
|
|



 2003 McGraw-Hill Higher Education
2003 McGraw-Hill Higher Education