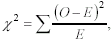|  Statistics for the Behavioral Sciences, 4/e Michael Thorne,
Mississippi State University -- Mississippi State
Martin Giesen,
Mississippi State University -- Mississippi State
Chi Square
Chapter OverviewPrevious chapters have detailed the t test and the F test, both of which are parametric methods. Parametric
tests examine hypotheses about population parameters such as µ and σ, usually assume at least interval
scale measurement, and assume a normal distribution of the measured variable in the population from
which samples were drawn. The chi-square test is called a nonparametric test because population
parameters are not estimated. It is also a distribution-free test because no particular population distribution
is assumed. The chi-square test is particularly useful with nominal scale or categorical data -- data in which
there are only frequencies of occurrence.
A chi-square test on a single categorical variable is called a goodness-of-fit test. The formula for the
goodness-of-fit test is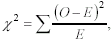 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55323/chap14a.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a>
where O is the observed frequency and E is the expected frequency. If the expected frequencies are
assumed to be equally distributed across the levels of the categorical variable, then the total number of
observations (N) is divided by the number of categories to determine E for each category. Expected
frequencies may also be determined by assigning the frequencies on the basis of percentages obtained in
previous research. The c2 computed for the goodness-of-fit test is compared with critical values from Table
G (see Appendix 2) with df = K - 1, where K is the number of levels of the categorical variable. The chisquare
goodness-of-fit test can sometimes be used to confirm the research hypothesis.
The chi-square test for different levels of two categorical variables is called the chi-square test of
independence, the two-sample chi square, or the chi-square test of significance. The test assumes that the
distribution of frequencies across the levels of one variable is the same for all levels of the other variable;
that is, the test assumes that the two categorical variables are independent. The formula for the chi-square
test of independence is the same as for the goodness-of-fit test. Expected frequencies may be given by
theory or previous research. Most often, however, they must be computed. Expected frequencies for a given
cell in a frequency table are computed by dividing the product of the marginal totals for the cell by the total
number of observations. The computed c2 is compared with critical values from Table G with df =
(R - 1)(C - 1), where R is the number of rows and C is the number of columns.
The chi-square test can be used only with frequency data. However, any data can be converted to
frequency data by dividing the data into several logical categories and counting the number of observations
that occur in each category.
A second restriction on chi square is that the individual observations must be independent of one
another. Another restriction is that if you are recording whether an event occurs, you must have in the data
both the frequency of occurrence and the frequency of nonoccurrence. Also, no expected frequencies
should be less than 5, although the restriction may be relaxed if there are more than four cells and only a
few have expected frequencies less than 5. Although there is a statistical alternative to c2 with a 2 x 2 table
and expected frequencies less than 5, the best approach is to test more subjects to increase the expected
frequencies. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif:: ::/sites/dl/free/0072832517/55323/chap14a.gif','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a>
where O is the observed frequency and E is the expected frequency. If the expected frequencies are
assumed to be equally distributed across the levels of the categorical variable, then the total number of
observations (N) is divided by the number of categories to determine E for each category. Expected
frequencies may also be determined by assigning the frequencies on the basis of percentages obtained in
previous research. The c2 computed for the goodness-of-fit test is compared with critical values from Table
G (see Appendix 2) with df = K - 1, where K is the number of levels of the categorical variable. The chisquare
goodness-of-fit test can sometimes be used to confirm the research hypothesis.
The chi-square test for different levels of two categorical variables is called the chi-square test of
independence, the two-sample chi square, or the chi-square test of significance. The test assumes that the
distribution of frequencies across the levels of one variable is the same for all levels of the other variable;
that is, the test assumes that the two categorical variables are independent. The formula for the chi-square
test of independence is the same as for the goodness-of-fit test. Expected frequencies may be given by
theory or previous research. Most often, however, they must be computed. Expected frequencies for a given
cell in a frequency table are computed by dividing the product of the marginal totals for the cell by the total
number of observations. The computed c2 is compared with critical values from Table G with df =
(R - 1)(C - 1), where R is the number of rows and C is the number of columns.
The chi-square test can be used only with frequency data. However, any data can be converted to
frequency data by dividing the data into several logical categories and counting the number of observations
that occur in each category.
A second restriction on chi square is that the individual observations must be independent of one
another. Another restriction is that if you are recording whether an event occurs, you must have in the data
both the frequency of occurrence and the frequency of nonoccurrence. Also, no expected frequencies
should be less than 5, although the restriction may be relaxed if there are more than four cells and only a
few have expected frequencies less than 5. Although there is a statistical alternative to c2 with a 2 x 2 table
and expected frequencies less than 5, the best approach is to test more subjects to increase the expected
frequencies. |
|



 2003 McGraw-Hill Higher Education
2003 McGraw-Hill Higher Education