Problem:

Suppose the market for watermelons can be described by the graph below.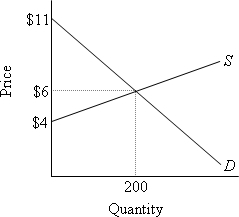

<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0077337727/883732/ch05_01.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a>

1. If Jon is willing to pay as much as $8 for a watermelon, how much surplus would he receive if he pays the market price for a watermelon?
2. Suppose Figgy Farms requires at least $5 per watermelon to be willing to sell in this market. What is Figgy's producer surplus for one watermelon in this market?
3. How much total consumer surplus is received in this market?
4. How much total producer surplus is received in this market?
5. What is the total surplus (combined consumer and producer surplus) in the market?

Answer:

1. Consumer surplus is the difference between the maximum Jon is willing to pay and the price he actually pays. The equilibrium price in this market is $6, so his consumer surplus is $2. $2 = $8 – $6.
2. Producer surplus is the difference between the market price and the minimum a seller requires to offer the product for sale. In this case, Figgy's producer surplus is $6 – $5 = $1.
3. Total consumer surplus is the area below the demand curve but above the market price. The area of this triangle on the graph is ½ x ($11 – $6) x 200 = $500.
4. Total producer surplus is the area above the supply curve but below the market price. The area of this triangle on the graph is ½ x ($6 – $4) x 200 = $200.
5. The total surplus is the sum of consumer and producer surplus, or $500 + $200 = $700.

Problem:

Three individuals' demand schedules for a good are shown in the table below. Assume these are the only individuals in the society.

1. If this is a private good, what is the total quantity demanded at a price of $13? What is the total quantity demanded at a price of $11?
2. Assuming this is a private good whose marginal cost is constant and equal to $10, determine the optimal or efficient quantity of the good.
3. Now assume this is a public good. What is the marginal benefit of the second unit of this good? What is the marginal benefit of the third unit? The fourth unit?
4. If the marginal cost is constant and equal to $30, determine the optimal or efficient quantity of this public good.

Answer:

1. For a private good, the total quantity demanded is the sum of the quantities demanded by each of the three individuals at a given price. At a price of $13, the total quantity demanded is 3: 2 from Lynn, 0 from Mark, and 1 from Pete. At a price of $11, the total quantity demanded is 4 + 1 + 3 = 8.
2. The optimal amount occurs where price and marginal cost are equal. Since marginal cost is $10, price must be $10. At this price, the total quantity demanded is 5 + 2 + 4 = 11 units.
3. The marginal benefit of any particular unit is the sum of the values placed on that unit by each of the individuals. In this example, the marginal benefit of the second unit is $35: $13 by Lynn, $10 by Mark, and $12 by Pete. The marginal benefit of the third unit is $12 + $9 + $11 = $32. The marginal benefit of the fourth unit is $11 + $8 + $10 = $29.
4. Comparing marginal benefit to marginal cost, the third unit should be provided, as its marginal benefit of $32 exceeds its marginal cost of $30. However, the fourth unit should not be provided as its marginal benefit is less than its marginal cost: $29 < $30.