 |
| 1 |  | 
The sampling distribution of 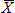 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> must be a normal distribution with a mean 0 and standard deviation 1. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> must be a normal distribution with a mean 0 and standard deviation 1. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 2 |  | 
A sample statistic is an unbiased point estimate of a population parameter if the mean of the population of all possible values of the statistic equals the population parameter. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 3 |  | 
The standard deviation of all possible sample proportions increases as the sample size increases. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 4 |  | 
The Central Limit Theorem states that as sample size increases, the population distribution more closely approximates a normal distribution. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 5 |  | 
The population of all possible sample proportions approximates a normal distribution if the sample size n is large. "n" should be considered large if np and n(1 - p) are |
|  | A) | Greater than 30. |
|  | B) | At least 5. |
|  | C) | Greater than 0. |
|  | D) | Less than 100. |
|  | E) | At least 25. |
|
|
 |
| 6 |  | 
For nonnormal populations, as the sample size a(n) _________________, the distribution of sample means approaches a(n) ___________________ distribution. |
|  | A) | decreases, uniform |
|  | B) | increases, normal |
|  | C) | decreases, normal |
|  | D) | increases, uniform |
|  | E) | increases, exponential |
|
|
 |
| 7 |  | 
As the sample size _____________, the variation of the sampling distribution of 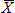 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> __________________. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> __________________. |
|  | A) | decreases, decreases |
|  | B) | increases, remains the same |
|  | C) | decreases, remains the same |
|  | D) | increases, decreases |
|
|
 |
| 8 |  | 
If the sampled population has mean 48 and standard deviation 16, then the mean and the standard deviation for the sampling distribution of 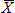 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> for n = 16 are <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> for n = 16 are |
|  | A) | 4 and 1. |
|  | B) | 12 and 4. |
|  | C) | 48 and 4. |
|  | D) | 48 and 1. |
|  | E) | 48 and 16. |
|
|
 |
| 9 |  | 
In order to take a random sample, we must have a frame of all the population elements. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 10 |  | 
If the population proportion is .4 with a sample size of 20, then this sample is large enough so that the sampling distribution of 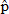 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036567/ch7_10q.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> is a normal distribution. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036567/ch7_10q.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> is a normal distribution. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 11 |  | 
Whenever the sampled population has a normal distribution, the sampling distribution of 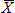 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> is a normal distribution <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> is a normal distribution |
|  | A) | for only large sample sizes. |
|  | B) | for only small sample sizes. |
|  | C) | for any sample size. |
|  | D) | for only samples of size 30 or more. |
|
|
 |
| 12 |  | 
If in a sampling distribution of 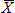 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> the sample size is 25, what assumption must hold for the sampling distribution of <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> the sample size is 25, what assumption must hold for the sampling distribution of 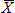 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> to be normal? <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036571/ch7_q1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (11.0K)</a> to be normal? |
|  | A) | Population distribution is normal. |
|  | B) | 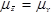 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/formu1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (14.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/formu1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (14.0K)</a> |
|  | C) | Population distribution is uniform. |
|  | D) | 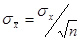 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/formu2.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/formu2.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (15.0K)</a> |
|
|
 |
| 13 |  | 
A random sample of size 36 is taken from a normal population with a mean of 50 and a standard deviation of 5. What is the sample standard deviation? |
|  | A) | 5/36 |
|  | B) | 36/50 |
|  | C) | 5/6 |
|  | D) | 6/36 |
|  | E) | 5/1 |
|
|
 |
| 14 |  | 
The Central Limit Theorem allows for estimating the sampling distribution of sample means when the sample size is small. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 15 |  | 
Strata are overlapping groups from the population to make a stratified random sample. |
|  | A) | True |
|  | B) | False |
|
|

