 |
| 1 |  | 
When the sample size and sample standard deviation remain the same, a 99 percent confidence interval for a population mean, µ, will be ______ the 95 percent confidence interval for µ. |
|  | A) | wider than |
|  | B) | narrower than |
|  | C) | equal to |
|
|
 |
| 2 |  | 
When the level of confidence and sample standard deviation remain the same, a confidence interval for a population mean based on a sample of n = 100 will be _______ a confidence interval for a population mean based on a sample of n = 50. |
|  | A) | wider than |
|  | B) | narrower than |
|  | C) | equal to |
|
|
 |
| 3 |  | 
An 82 percent confidence interval for a sampling distribution with a mean of 100, a population standard deviation of 24, and a sample size of 36 will be based on an α = ______ and a corresponding Zα/2 of ________. |
|  | A) | .18 and .47 |
|  | B) | .09 and .915 |
|  | C) | .09 and .23 |
|  | D) | .18 and 1.34 |
|
|
 |
| 4 |  | 
When finding a confidence interval for a population mean, the probability that the confidence interval will contain the population mean is called the ______________. |
|  | A) | margin of error |
|  | B) | confidence coefficient |
|  | C) | t distribution |
|  | D) | degrees of freedom |
|
|
 |
| 5 |  | 
When the level of confidence and sample proportion 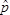 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/p_cap.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (13.0K)</a> remain the same, a confidence interval for a population proportion p based on a sample of n = 100 will be _________ a confidence interval for p based on a sample of n = 400. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/p_cap.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (13.0K)</a> remain the same, a confidence interval for a population proportion p based on a sample of n = 100 will be _________ a confidence interval for p based on a sample of n = 400. |
|  | A) | wider than |
|  | B) | narrower than |
|  | C) | equal to |
|
|
 |
| 6 |  | 
As our sample standard deviation increases when all other parts of the confidence interval stay the same, then the confidence interval will |
|  | A) | become wider. |
|  | B) | become narrower. |
|  | C) | remain the same. |
|
|
 |
| 7 |  | 
When the population is normally distributed and the population standard deviation σ is unknown, then for any sample size n, the sampling distribution of 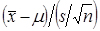 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/formu3.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (17.0K)</a> is a t distribution. <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/formu3.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (17.0K)</a> is a t distribution. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 8 |  | 
When the population is normally distributed, population standard deviation σ is unknown, and the sample size is n = 15, the confidence interval for the population mean µ is based on |
|  | A) | the z (normal) distribution. |
|  | B) | the t distribution. |
|  | C) | the binomial distribution. |
|  | D) | the Poisson Distribution. |
|  | E) | None of the above. |
|
|
 |
| 9 |  | 
When solving for the sample size needed to compute a confidence interval for a population proportion, the ________ p(1 - p) is, the ________ n will be. |
|  | A) | larger, smaller. |
|  | B) | smaller, larger. |
|  | C) | larger, larger. |
|
|
 |
| 10 |  | 
When a confidence interval for a population proportion is constructed for a sample size n = 100 and the value of 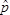 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/p_cap.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (13.0K)</a> = .4, the interval is based on <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0078020530/1036570/p_cap.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (13.0K)</a> = .4, the interval is based on |
|  | A) | the z distribution. |
|  | B) | the t distribution. |
|  | C) | the exponential distribution. |
|  | D) | the Poisson distribution. |
|  | E) | None of the above. |
|
|
 |
| 11 |  | 
Assuming the same value of α, as the sample size increases, the value of tα/2 approaches the value of Zα/2. |
|  | A) | True |
|  | B) | False |
|
|
 |
| 12 |  | 
There is little difference between the values of tα/2 and Zα/2 when the sample |
|  | A) | size is small. |
|  | B) | size is large. |
|  | C) | mean is small. |
|  | D) | mean is large. |
|  | E) | standard deviation is small. |
|
|
 |
| 13 |  | 
When determining the sample size n, if the value found is not an integer initially, we _______ round this value up to the next integer value. |
|  | A) | always |
|  | B) | sometimes |
|  | C) | never |
|
|
 |
| 14 |  | 
______ is the quantity that is added to or subtracted from a point estimate of a population parameter to obtain a confidence interval. |
|  | A) | The standard error |
|  | B) | The sample standard deviation |
|  | C) | t |
|  | D) | The margin of error |
|
|
 |
| 15 |  | 
Confidence intervals are different from tolerance intervals. |
|  | A) | True |
|  | B) | False |
|
|

