The Mathematics Test consists of two parts: Part I examines a test-taker’s ability to solve problems with complex calculations in realistic settings. The Casio fx-260 scientific calculator is provided to aid with calculations for this part of the test. The calculator is not provided for Part II, which examines a test-taker’s ability to solve problems using estimation, mental math, and paper and pencil. Cognitive Levels and Content AreasBoth parts of the Mathematics Test contain 25 items that are drawn from the following content areas and skills: NUMBER OPERATIONS AND NUMBER SENSE (20–30%)- Representing and using numbers in a variety of equivalent forms (integer, fraction, decimal, percent, exponential, and scientific) in real world and mathematical problem situations
- Using number sense for whole numbers, fractions, decimals, integers, and rational numbers
- Analyzing, explaining, and applying ratios, proportions, and percents in a wide variety of situations
- Using order relations for whole numbers, fractions, decimals, integers, and rational numbers
- Selecting the appropriate operation to represent problem situations
- Relating the basic arithmetic operations to one another
- Computing with whole numbers, fractions, decimals, and integers (with a calculator, with no restrictions, and mentally or with pencil and paper with certain restrictions)
- Using, analyzing, and explaining procedures for making estimates with whole numbers, fractions, decimals, percents, and square roots
- Using estimation to solve problems and to assess the reasonableness of the answer
MEASUREMENT AND GEOMETRY (20–30%)- Modeling and solving problems using the concepts of perpendicularity, parallelism, congruence, and similarity of geometric figures
- Using spatial visualization to describe and analyze geometric figures
- Using the Pythagorean Theorem and similarity to model and solve problems
- Finding, using, and interpreting the slope of a line, the y-intercept of a line, and the intersection of two lines
- Using coordinates to design and describe geometric figures or translations/rotations of geometric figures
- Identifying and selecting appropriate units of metric and customary measures
- Converting and estimating units of metric and customary measure
- Solving and estimating solutions to problems involving length, perimeter, area, surface area, volume, angle measurement, capacity, weight, and mass
- Using uniform rates in problem situations
- Reading and interpreting scales, meters, and gauges
- Predicting the impact of changes in linear dimension on the perimeter, area, and volume of figures
DATA ANALYSIS, STATISTICS, AND PROBABILITY (20–30%)- Constructing, interpreting, and drawing inferences from tables, charts, and graphs
- Making inferences and convincing arguments that are based on data analysis
- Evaluating arguments that are based on data analysis, including distinguishing between correlation and causation
- Representing data graphically in ways that make sense and are appropriate to the context
- Applying measures of central tendency (mean, medium, mode) and analyzing the effect of changes in data on these measures
- Using an informal line of best fit to predict from data
- Applying and recognizing the role of sampling and the impact of bias on statistical claims
- Making predictions that are based on experimental or theoretical probabilities, including listing possible outcomes
- Using and interpreting a frequency distribution of outcomes
- Comparing and contrasting different sets of data on the basis of measures of central tendency and dispersion
ALGEBRA, FUNCTIONS, AND PATTERNS (20–30%)- Analyzing and representing situations involving variable quantities with tables, graphs, verbal descriptions, and equations
- Recognizing that a variety of problem situations may be modeled by the same function or type of function
- Converting between different representations, such as tables, graphs, verbal descriptions, and equations
- Creating and using algebraic expressions and equations to model situations and solve problems
- Evaluating formulas and functions
- Solving equations and systems of linear equations
- Recognizing and using direct and indirect variation
- Analyzing tables and graphs to identify and generalize patterns and relationships
- Analyzing and using functional relationships to explain how a change in one quantity results in change in the other quantity, including linear, quadratic, and exponential functions
Test items also examine a test-taker’s capabilities at the following cognitive levels: PROCEDURAL (15–25%)- Selecting and applying appropriate procedures correctly
- Verifying and justifying the correctness of a procedure using concrete models or symbolic methods
- Extending or modifying procedures to deal with factors inherent in problem settings
- Using numerical algorithms
- Reading and producing graphs and tables
- Executing geometric constructions
- Rounding numbers appropriately, including rounding up/down to represent a whole number answer as appropriate in a problem situation
- Ordering lists of numbers
CONCEPTUAL (25–35%)- Recognizing concepts
- Labeling concepts
- Generating examples and/or counter examples of concepts
- Interrelating models, diagrams, and representatives of concepts
- Identifying and applying principles
- Knowing and applying facts and definitions
- Comparing, contrasting, and integrating related concepts and principles
- Recognizing, interpreting, and applying signs, symbols, and terms
- Interpreting assumptions and relations
APPLICATION/MODELING/PROBLEM SOLVING (50%)- Recognizing and formulating problems
- Determining the sufficiency and consistency of data
- Using strategies, data, models, and relevant math
- Generating, extending, and modifying procedures
- Judging the reasonableness and correctness of solutions
Context and FormatMost of the items on the Mathematics Test are based on realistic applications with which test-takers have had considerable experience, such as the world of work, the consumer, technology, and family experiences. A small number of items involve specific applications of mathematical concepts in a non-contextual situation. Approximately 50 percent of the items are based on graphics, and 25 percent of the items are set-up questions, in which the test-taker needs to determine how to solve a problem but not necessarily calculate the results. In approximately 4 percent of the questions, one answer option may be “not enough information is given.” While most of the items on the test are multiple-choice, there are also two unique “alternate format” grids that are used on each part of the test: THE NUMBER GRIDThe number grid contains five blanks above a column of numbers and symbols. To answer the question on a number grid, test-takers must write the correct answer in the blank boxes at the top of each column. A separate column must be used for each digit. Then the appropriate circle must be filled in below each box. Below is an example of a mathematics item with a number grid: Find the quotient of 5513 divided by 37. Then round the answer to the nearest ten and mark the rounded quotient on the number grid.
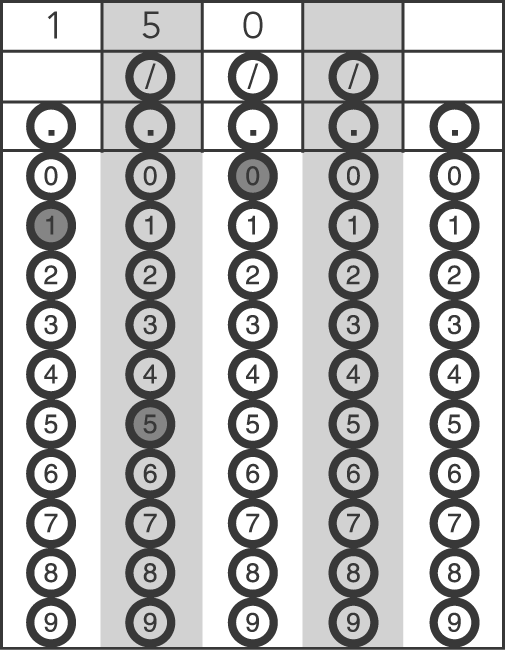 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Number Grid::/sites/dl/free/0809222329/45405/NumberGrid.gif','popWin', 'width=166,height=216,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Number Grid (38.0K)</a>Number Grid <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Number Grid::/sites/dl/free/0809222329/45405/NumberGrid.gif','popWin', 'width=166,height=216,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Number Grid (38.0K)</a>Number GridThe correct answer to this problem is 150 (5513 ÷ 37 = 149, which rounds to 150), which has been filled in on the number grid above. The answer on the number grid may begin in the first column on the left (as above), may end in the last column on the right, or may be centered in the columns. There are six number grid problems on Part I of the Mathematics Test and two number grid problems on Part II. THE COORDINATE PLANE GRIDThe second form of alternate format grid is the coordinate plane grid. This answer grid resembles the coordinate plane with small circles where test-takers’ can mark the position of a point. Below is an example of a mathematics item with a coordinate plane grid: Find the y-intercept of the equation y = x + 4. Mark your answer on the coordinate plane grid.
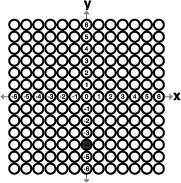 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Coordinate Plane Grid::/sites/dl/free/0809222329/45405/CoordinateGrid.gif','popWin', 'width=216,height=216,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Coordinate Plane Grid (8.0K)</a>Coordinate Plane Grid <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=gif::Coordinate Plane Grid::/sites/dl/free/0809222329/45405/CoordinateGrid.gif','popWin', 'width=216,height=216,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif">Coordinate Plane Grid (8.0K)</a>Coordinate Plane GridThere is one coordinate plane grid on each part of the Mathematics Test. |



 2002 McGraw-Hill Higher Education
2002 McGraw-Hill Higher Education

 2002 McGraw-Hill Higher Education
2002 McGraw-Hill Higher Education