Commonly, water waves are generated by wind blowing across the surface of the ocean or other body of water. Much is known regarding the physics governing the behavior of these waves and the information below provides a succinct summary of the fundamental principles of water waves. The discussion that follows is summarized from An Introduction to the World's Oceans, 8th edition by K.A. Sverdrup, A.C. Duxbury, and A.B. Duxbury (2004).

First, it is appropriate to review some basic terminology associated with wave phenomena. The diagram below illustrates a variety of terms used to describe water waves.

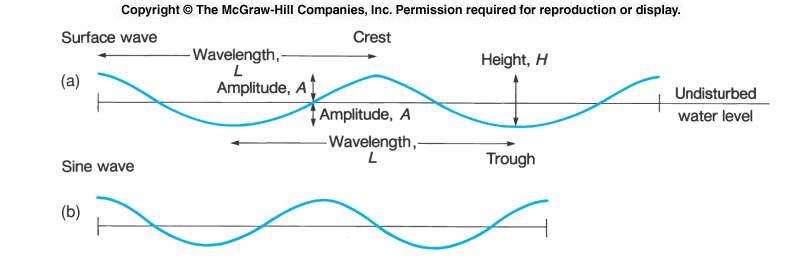
In the image above, (a) shows a schematic of an idealized water wave generated by wind blowing across the surface of the ocean. Note that the shape of this wave approximates a sine wave (b) but is not precisely the same. Terms in the diagram are defined below:

Wave Crest: is the highest portion of the wave.
Wave Trough: is the lowest portion of the wave.
Wavelength: is the linear distance separating wave crests (or separating wave troughs).
Wave Amplitude: is the displacement of a crest or trough about the mean position or an undisturbed water level.
Wave Height: is the total vertical distance from crest to trough (equal to twice the amplitude).
Wave Period: is the time required for successive wave crests (or troughs) to pass a fixed point.

Deep-Water Waves, Shallow-Water Waves, and Wave Speed (or Celerity):

In the open ocean, wind-generated waves are defined as deep-water waves because water depth is greater than one-half the waves' length. When these waves enter water where the depth becomes shallower than 1/20th of the wavelength, then the waves are defined as shallow-water waves. The distinction between deep-water waves and shallow-water waves has important implications for the behavior of these waves, especially as it is affects wave speed (or celerity).

Deep-water waves propagate across the ocean at celerity (C) that is determined by the product of a constant and the wave period (T):

C = 1.56 x T

In contrast, shallow-water waves propagate with celerity (C) equal to the product of a constant (3.13) and the square root of water depth (D):

C = 3.31 x D^0.5

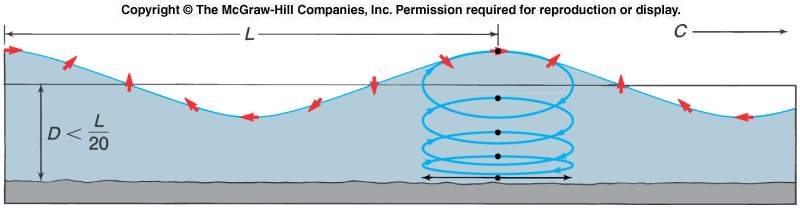
The displacement of water particles by deep-water and shallow-water waves also varies. In deep water, the passage of waves induces circular orbits of particles. The radius of these orbits decreases with depth until wave displacement ceases at a depth equal to one-half the wavelength (see illustration below).

For shallow-water waves, interaction of the wave with the seafloor causes the circular orbits to be deformed into ellipses (see below). In extremely shallow water, these ellipses are nearly flat, giving rise to particle motion that is almost entirely translational (back and forth).

The phenomena described by the figures above are very nicely illustrated with an interactive applet created by Dr. R.A. Dalrymple at the University of Delaware. Follow the link below to create visualizations of the motion of both deep-water and shallow-water waves by choosing appropriate periods, wave heights, and water depths.

Comparison of Wind Waves and Tsunamis:

The images below comparatively illustrate fundamental features of typical wind-generated waves and tsunamis using graphics derived from the Linear Wave Kinematics Applet of Dr. R.A. Dalrymple at the University of Delaware.

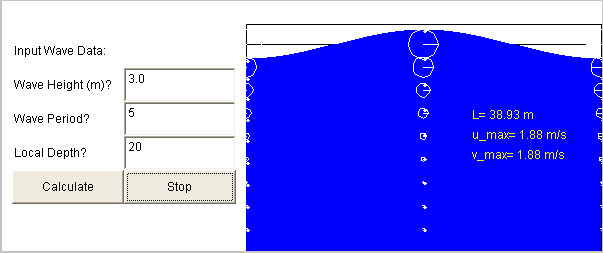
The image above shows the wave height, wavelength (L), wave period, and displacement orbits for a wave with 3-m wave height traveling in water 20 m deep. Note the circular displacement orbits. For the calculated wavelength (approximately 39 m), wave displacement would cease at approximately 19 m depth. This graphic is scaled so that the width of the plot equals the wavelength and the height of the plot equals the water depth (resulting in significant distortion).

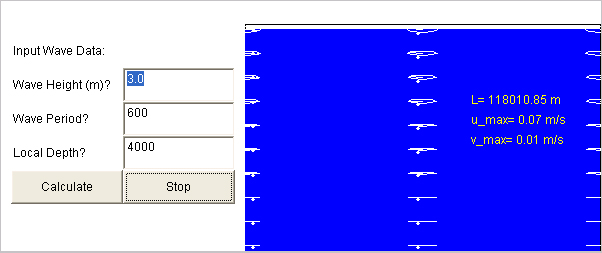
This image above shows displacement orbits for a tsunami with wave height = 3 m, period of 600 seconds (10 minutes) traveling through water 4,000 m deep. Note the calculated wavelength (L) is 118 km and the displacement orbits are ellipses of very high eccentricity (nearly flat). Note also that particle displacement extends to the bottom of the ocean (in this instance 4,000 m). This plot is also scaled so that the width of the plot is the wavelength and the height of the plot is the water depth (resulting in significant distortion). Finally, note on this plot that the amplitude of the tsunami is not discernable at the surface.

Wave Refraction and Diffraction:

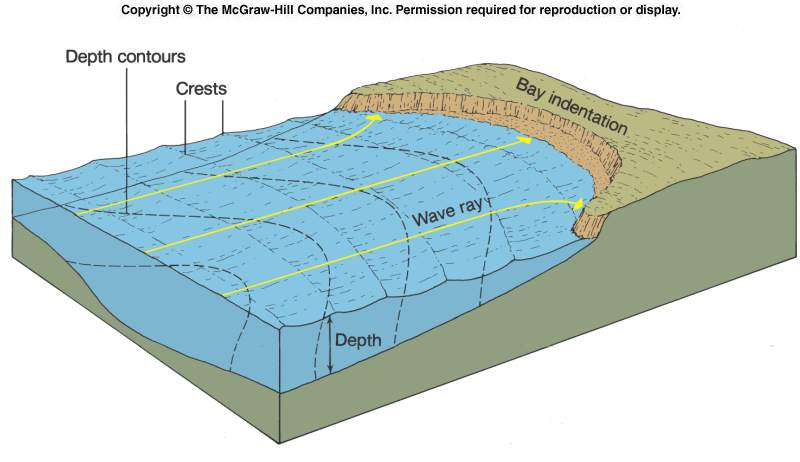
Wave Refraction refers to the phenomenon commonly observed when waves enter shallow water over irregular seafloor topography. Those portions of the wave traveling in the shallowest water will also move with the slowest celerity (can you determine why based on the discussion above?). While portions of the wave in deeper water continue moving with relatively greater celerity, the wave crests will be observed to curve or refract as the wave moves forward (see image below).

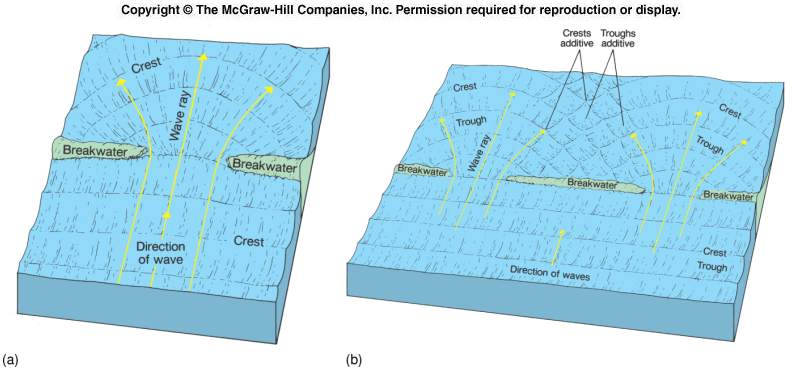
Similarly, when waves approach barriers with gaps as in illustration (a) below, the wave will be observed to spread or disperse upon passing through the gap. This process is called "wave diffraction". If waves approach a barrier with multiple gaps as in illustration (b) below, wave diffraction will occur as the wave passes through each gap, and the spreading waves may interact both destructively and constructively. Thus, barriers with many gaps can efficiently scatter wave energy, often diminishing the height and power of waves.

Tsunamis (as virtually everyone knows by now) are a series of waves generated by displacement of the ocean water column by impulsive events. Events known to generate tsunamis are submarine earthquakes, explosive volcanic eruptions, submarine landslides, terrestrial landslides that enter water bodies, and impacts of large extraterrestrial objects (e.g. asteroids or comets) in the ocean.

Tsunamis differ from typical wind-generated waves in that they have very long wavelengths and periods. Wavelengths for tsunamis may range from 100 to 200 km (100,000 to 200,000 m) and periods may range from 20 - 40 minutes. Because the wavelength of a tsunami is so long, it is characterized as a shallow-water wave, even as it traverses the open ocean. For example, a tsunami with a wavelength of 100,000 m will behave as a shallow-water wave in water that is up to 5,000 m deep because 5,000 m is 1/20th of the wavelength of the tsunami.

Though tsunamis have very long wavelengths, their amplitude in the open ocean is often relatively small - commonly only a meter or two - and this amplitude is distributed over the very long wavelength so that tsunamis are quite imperceptible on the surface of the ocean.

Since tsunamis are shallow water waves, their celerity is governed by the shallow-water wave celerity equation:

such that their speed is directly proportional to the square root of water depth. However, in the open ocean, the relatively great depth of water yields spectacular speed for tsunamis. For example, a tsunami travelling across an ocean basin with average depth 4,000 m will move forward at C = 3.31 x (4,000)^0.5 = 209 m per second. This is equivalent to approximately 750 km/hr or 465 miles per hour!

Tsunami energy also dissipates very slowly, so they may travel across an entire ocean basin and even reflect from the opposite shore to travel across the ocean several more times.

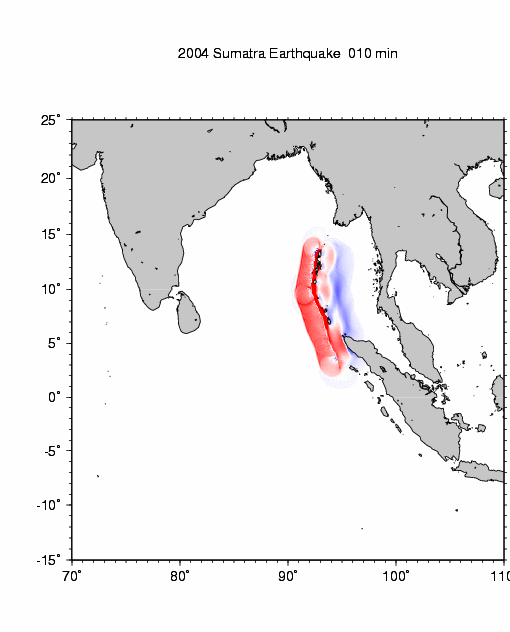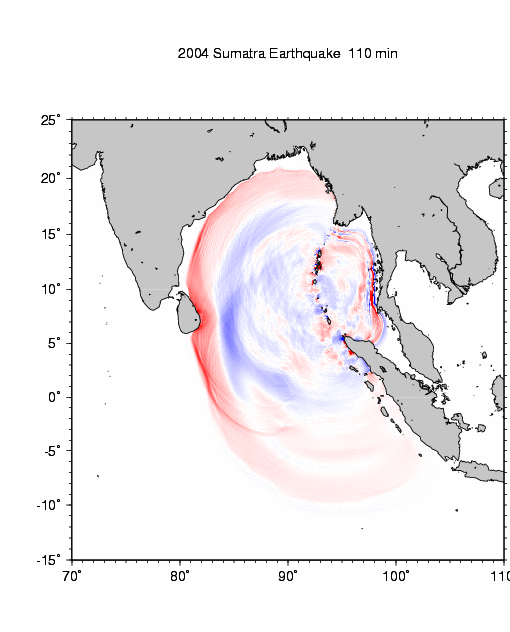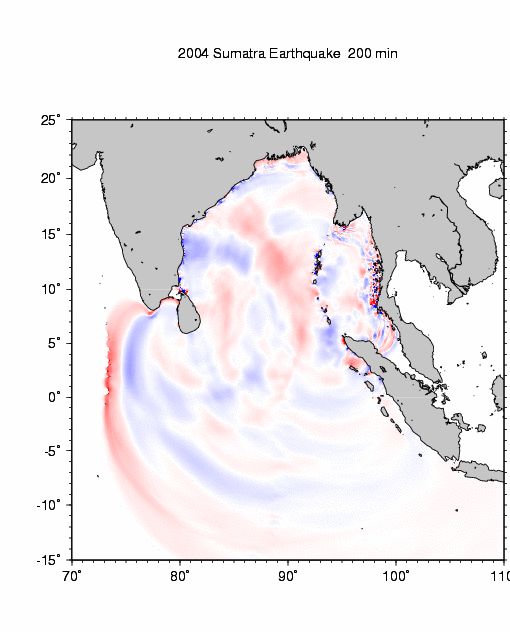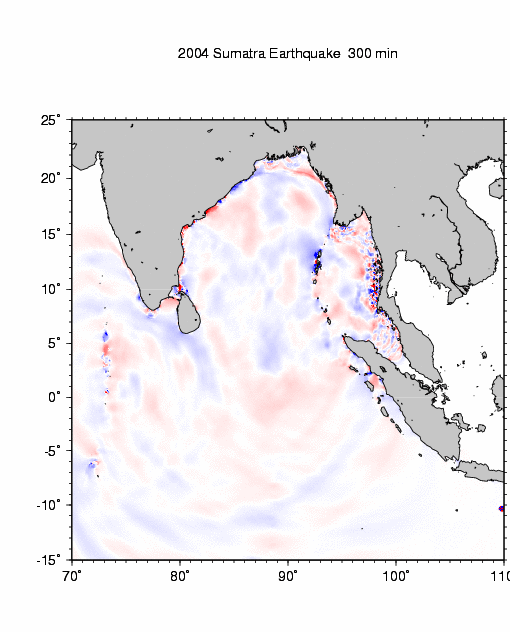
Below, examine the animation derived from numerical simulation of the tsunami of 26 December 2004. This animation was produced from a computer model by Dr. Kenji Satake of the National Institute of Advanced Industrial Science and Technology (AIST), Japan. (If the animation is not running, click the "Refresh" button on your browser or click on the image to view the animation directly on Dr. Satake's web site). Red color on this animation represents wave crests; blue represents wave troughs.

Numerical simulation of tsunami of 26 December 2004
by Dr. Kenji Satake, Geological Survey of Japan, AIST, National Institute of Advanced Industrial Science and Technology (AIST), Japan

Observe refraction of the tsunami as slower-moving portions of the wave propagate around the ocean margins while faster-moving portions propagate across the central Indian Ocean. Wave refraction is particularly evident as the tsunami wraps around the coasts of Sri Lanka and southern India. The primary westbound wave is also observed to reflect from the island of Sri Lanka and propagate northeast, eventually making landfall along the coasts of Bangladesh and Myanmar. Also note the patterns of wave diffraction as the wave interacts with island chains (essentially barriers with narrow gaps) in both the eastern and western Indian Ocean. Patterns of both constuctive and destructive interference are evident in the diffracted waves. Finally, note the celerity of the eastbound wave (toward the Malay Peninsula) and the westbound wave (toward Sri Lanka). Because of the great difference in water depth across the central Indian Ocean relative to the Andaman Sea, waves emanating from the source region in the Andaman-Nicobar Islands make landfall in Sri Lanka and Thailand at approximately the same time, despite having traveled very different distances.