The Investigation poses questions to generate interest in various
mathematical topics from the text and encourages students to formulate and investigate their
own conjectures. One use of the investigations is for term papers in which students report on
their conjectures and the patterns they find.
Click on the Read Me file below to open the investigation in a Word file:
 Read Me - Consecutive Numbers Instructions (Word Format)
(280.0K)
The Math Investigator is a data collection software program that may be used to collect data for the investigation. You may type answers onto the Word file or copy
and paste in data from the Investigator. Click here to launch the Consecutive Numbers Investigator
Math Investigator 2.1
CONSECUTIVE NUMBERS on the Math Investigator determines the ways, if any, that a number can be written as the sum of two or more nonzero consecutive whole numbers.
The number 18 can be written as the sum of nonzero consecutive whole numbers in two ways: 3 + 4 + 5 + 6 and 5 + 6 + 7 Consecutive numbers can be illustrated by columns of tiles as shown here. 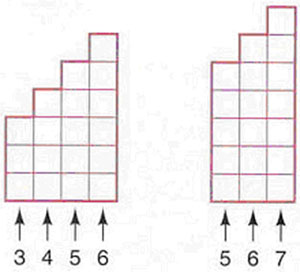 <![CDATA[<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78560/2_1.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (30.0K)</a>]]> Starting Points for Investigations- Investigate the numbers from 1 to 50 to determine which numbers can or cannot be written as the sum of consecutive whole numbers. You may wish to print the sums from the computer to look for patterns. Based on your observations, form conjectures about which numbers can be written as the sum of nonzero consecutive numbers.
- What types of numbers can always be written as the sum of two nonzero consecutive whole numbers? Three nonzero consecutive whole numbers? Four nonzero consecutive whole numbers? etc.. Write conjectures about the types of numbers that can be written as the sums of nonzero consecutive whole numbers and test your conjectures for some numbers greater than 50.
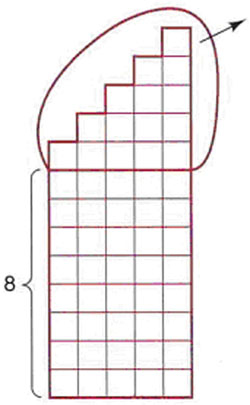
- The sums of nonzero consecutive whole numbers can be illustrated by columns of tiles, with each column increasing by one tile. The tiles for 9 +10 + 11 + 12 + 13 is shown below. Notice that there is a 1-to-5 staircase (triangular number) at the top of the column. If this staircase is removed, a rectangle remains whose height plus one is the first number, 9, of the sum of consecutive numbers. Form some sketches of other columns of tiles and investigate ways to use triangular numbers to determine if any given number can be written as a sum of nonzero consecutive numbers.
 <![CDATA[<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78560/2_1_2.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (32.0K)</a>]]> |
