| The Investigation poses questions to generate interest in various mathematical topics from the text and encourages students to formulate and investigate their own conjectures. One use of the investigations is for term papers in which students report on their conjectures and the patterns they find.
Click on the Read Me file below to open the investigation in a Word file:
 Read Me - Pyramid Patterns Instructions (Word Format)
(37.0K) Read Me - Pyramid Patterns Instructions (Word Format)
(37.0K)
Laboratory Investigation 9.3Pyramid Patterns
If the pattern in the figure below is traced and cut out, the triangular flaps can be folded up to form a pyramid whose apex is directly above point P. (That is, a line containing the apex and point P will be perpendicular to the base.) To construct these flaps, we must know the altitude h of the pyramid.
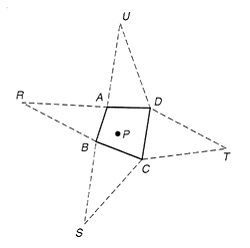 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_9_3a.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (21.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_9_3a.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (21.0K)</a>- For a given altitude, how were the vertex points R, S, T, and U determined? (Hint: The Pythagorean theorem is needed.)
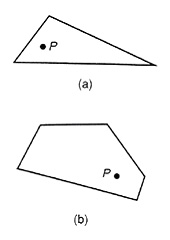
- Explain how triangular flaps can be constructed for any polygon and any point P in the same plane [see figures (a) and (b) below] so that the flaps fold up to form a pyramid of any given altitude with the apex directly above point P.
 <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_9_3b.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (19.0K)</a> <a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_9_3b.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (19.0K)</a> |


