Click on the Read Me file below to open the investigation in a Word file:

Read Me - Properties of Triangles Instructions (Word Format) (88.0K)

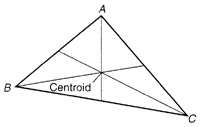
Computer Investigation 9.1

1. Each vertex of triangle ABC is connected to the midpoint of the opposite side of the triangle. These line segments are called medians and they intersect in a point called the centroid. The medians of a triangle subdivide a triangle into 6 smaller triangles. For any triangle, what can be said about the 6 small triangles that are obtained from the medians?
<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_9_1a.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (19.0K)</a>
a. Will any of these triangles be congruent?
b. Will any of their perimeters be equal?
c. Will any of their areas be equal?
d. Can the shape of the triangle be changed so that any of statements a-c will be true?

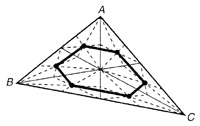
2. Consider the 6 small triangles which are formed by the medians of a triangle, as shown in the following figure. Suppose the centroids of each of these small triangles are used as the vertices of a hexagon. As ∆ ABC takes on various shapes, what can be said about this hexagon?
<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_9_1b.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (22.0K)</a>
a. Will any pairs of its sides be congruent?
b. Will any of its vertex angles be congruent?
c. Will it have any lines of symmetry?
d. Will it ever be a regular hexagon?

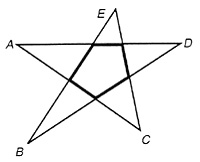
3. The following pentagon has had its sides extended to intersect in the points A, B, C, D, and E to form a 5-pointed star.
<a onClick="window.open('/olcweb/cgi/pluginpop.cgi?it=jpg::::/sites/dl/free/0072532947/78543/LI_9_1c.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="/olcweb/styles/shared/linkicons/image.gif"> (21.0K)</a>
a. What is the sum of the measures of the 5 angles whose vertices are A, B, C, D, E? Experiment with other convex pentagons. Is this sum the same for any convex pentagon that is used to form a 5-pointed star?
b. Form a 6-pointed star by extending the sides of a hexagon. What is the sum of the 6 angles at the 6 points of the star?
c. Continue this investigation for 7-pointed stars, 8-pointed stars, etc., and find a relationship in the sums of the measures of the angles at the points of the stars. State a conjecture regarding these sums.